人工神经网络(ANN)

一、机器学习基本概念与定理

#

1.1 基本概念

#

1.2 常用定理

#

1.3 数学基础

#

1.4 神经网络发展历史

#

第一次浪潮： 第二个迅猛发展：算法突破与架构创新
第三次浪潮：深度学习崛起与架构革命
第四次浪潮：大模型时代与多模态融合

二、人工神经网络（ANN）

#

2.1 定义：

#

• 神经网络是由具有适应性的简单单元组成的广泛并行互联的网络，它的 组织能够模拟生物神经系统对真实世界物体所作出的反应。
• 神经网络是由简单处理单元构成的大规模并行分布式处理器，天然地具 有存储经验知识和使之可用的特性。

2.2 生物神经元模型：

#

生物神经元是一个多输入、单输出的信息处理单元，单输出可以分枝为多个并行的相同输出，以便输入到其他神经元。

2.3 人工神经元

#

2.3.1 人工神经元结构

#

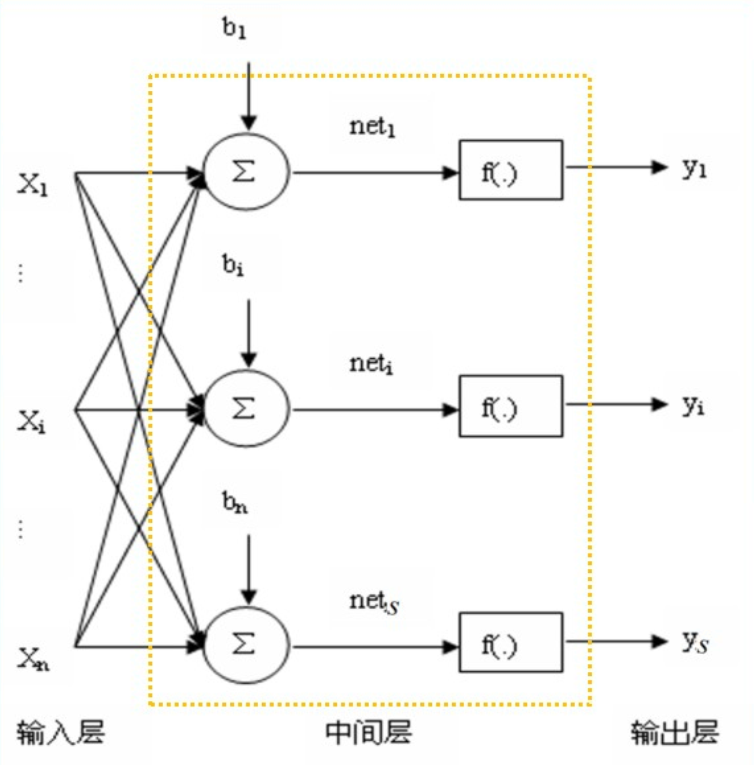
根据生物神经元抽象出人工神经元模型，基本结构：加权求和+非线性激励，即
累加器输出：$net_t=\sum^N_{j=1}\omega_{ij}+b_i$
网络输出：$y_i=f(net_t)$
其中，$w_{ij}$为输入的权值，$b_i$为偏置。
以上就是一个简单的单层感知机，具体参考单层感知机的介绍。
神经网络最核心的问题就是求网络的权值，方法是通过学习和训练。
激活函数的选取$f(\cdot)$的选取模拟了神经元的整合能力，提供了网络的非线性建模能力，常用的有

深度神经网络的采用ReLu函数作为激活函数，起到了防止梯度消失的作用。

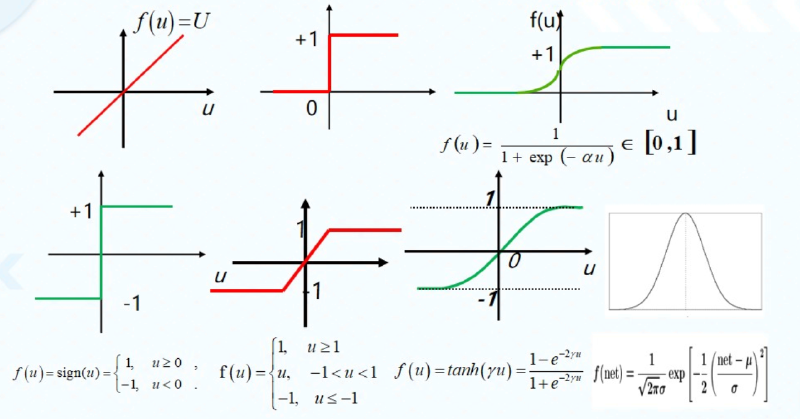
2.3.2 人工神经网络的数学描述

#

人工神经网络的结构可以用矩阵表示：
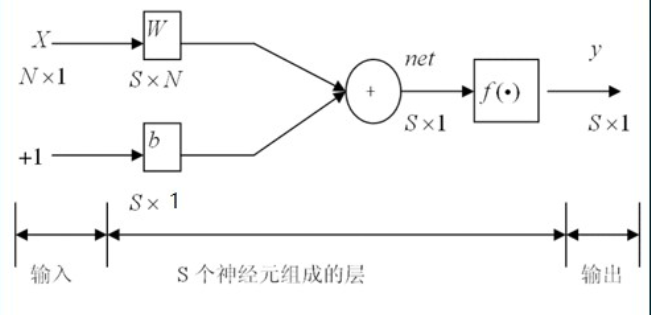
$net=W\cdot x+b, Y=f(net)=f(Wx+b)$，其中

$$ W = \begin{bmatrix} w_{11} & w_{12} & \cdots & w_{1n} \\ w_{21} & w_{22} & \cdots & w_{2n} \\ w_{s1} & w_{s2} & \cdots & w_{sn} \end{bmatrix} ,X= \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_s \end{bmatrix} ,b= \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_s \end{bmatrix} ,Net= \begin{bmatrix} net_1 \\ net_2 \\ \vdots \\ net_s \end{bmatrix} ,Y= \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_s \end{bmatrix} $$

用矩阵形式层级图表示为

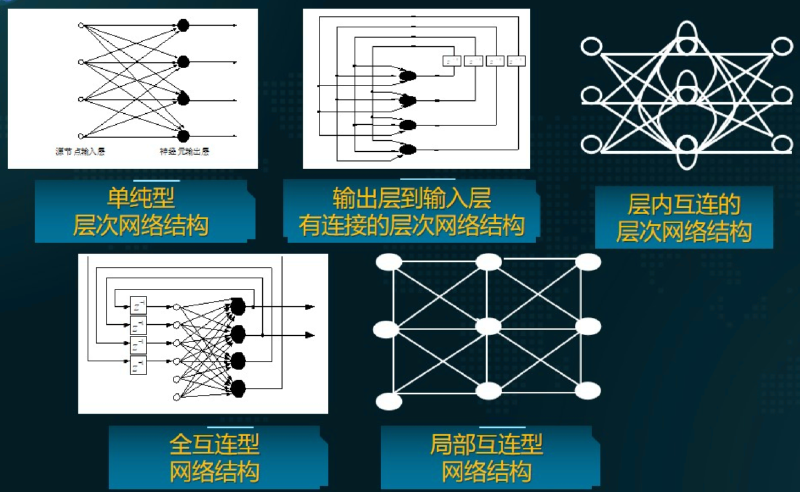
有了基本的人工神经元模型，可以构建出不同类型的人工神经网络，

三、基于自适应信号处理(ASP)的人工神经网络

#

定义输入矢量为：$X_k=[x_{0k},x_{1k},\cdots,x_{Nk}]^T$ 权矢量为：$W_k=[W_{0k},W_{1k},\cdots,W_{Nk}]^T$ ASP神经元输出为：$S_k=W^TX_k$ ASP神经元总输出为：$y_k=f(S_k)$ 线性误差为：$\epsilon_k=d_k-S_k=d_k-W^T\cdot X_k$ 均方误差为：$MSE=E{(d_k-W^T\cdot X_k)^2}$ 采用最小均方算法（梯度下降的优化算法），即LMS算法，改变权使得MSE达到极小。
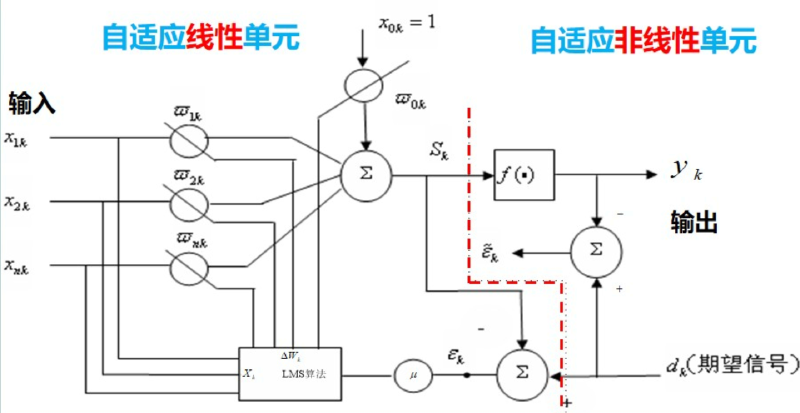
LMS算法：即最小均方算法(Least Mean Square)，是一种最陡算法的改进算法，该算法不需要已知输入信号和期望信号的统计特征，“当前时刻”的权系数是通过“上—时刻”权系统+—个负均方误差梯度的比例项求得。
新的权值$w_{k+1}=w_k+\mu\cdot(-\nabla_k)$ $\mu$是迭代步长/学习率，$\nabla_k=\frac{\partial MSE}{\partial w_k}$是梯度，带入MSE，得$\nabla_k=\frac{\partial}{\partial w_k}E(\epsilon^2_k)$ 工程上常用瞬时功率${\epsilon_k}^2$代替平均功率$E({\epsilon_k}^2)$，即
$MSE=E({\epsilon_k}^2)\approx{\epsilon_k}^2$

#

通过邮件回复